| Tue 10th July |
Wed 11th July |
Thu 12th July |
Fri 13th July |
Sat 14th July |
Sun 15th July |
Mon 16th July |
||
|---|---|---|---|---|---|---|---|---|
| 800 | 830 | Arrival | Breakfast | Breakfast | Breakfast | Breakfast | Breakfast | Breakfast |
| 900 | 1030 | Zoltán Donkó | Péter Nemes-Incze | Excursion | Endre Tóvári | Dezső Beke | Departure | |
| 1030 | 1100 | Break | Break | Break | Break | |||
| 1100 | 1230 | László Gránásy | Ferenc Simon | Péter Makk | Róbert Horváth | |||
| 1230 | 1300 | Lunch | Lunch | Lunch | Lunch | |||
| 1400 | 1630 | Gábor Ribárik | Katalin Kamaras | Dávid Szaller | Dezső Beke | |||
| 1630 | 1830 | Free time | Sport / Free time | Free time | Free time | |||
| 1800 | 1830 | Dinner | Dinner | Dinner | Dinner | Dinner | ||
| 1930 | 2030 | Plenary session | BBQ party | Sport / Free time | Game night | Plenary session Lajos Diósi | Plenary session | |
| 2030 | Welcome party | Party | Free night | Farewell party | ||||
Nanophysics section program committee:
- Dr. Peter Dusan Ispanovity, Eotvos University
- Dr. Janos Koltai, Eotvos University
- Dr. Andras Palyi, Eotvos University
- Zsolt Toth, Eotvos University
11th July
Zoltán Donkó: Molecular dynamics simulations of strongly coupled plasmas
Computer simulation methods represent a complementary approach
to experimental and theoretical studies and they have become invaluable tools
for the description of many-particle systems in numerous disciplines of science.
One of the main and widely applied approaches is the molecular dynamics
simulation, which makes it possible to trace the phase space tra jectories of
particles thereby providing information about the time-evolution of the systems
investigated. From the phase-space coordinates of the particles it is possible
to derive static, thermodynamic, as well as transport properties and to obtain
information about the collective excitations. The talk will review the basics
of equilibrium and non-equilibrium molecular dynamics methods and illustrate
their applications in studies of strongly coupled plasmas.
László Gránásy: From needle crystals to spherulites: Phase-field modeling of complex solidification morphologies
Field theoretic models of polycrystalline freezing will be reviewed. Two models will be presented: (i) A coarse-grained field theory, termed the phase-field (PF) model, and (ii) a simple dynamical density functional theory, known as the phase-field crystal (PFC) approach:
(i) The phase-field theory can be regarded as a multi-field generalization of the Cahn-Hilliard/Ginzburg-Landau type field theoretic models, in which the structural change during solidification is monitored by a structural order parameter, the phase field, whose time evolution is assumed to follow relaxation dynamics, and is coupled to the evolution of other conserved and/or non-conserved fields, such as temperature, concentration, or density. The phase-field model of polycrystalline freezing incorporates the phase-field, coupled to a concentration field, while differences in the crystallographic orientations are captured by an appropriate orientational field (scalar field in 2D and quaternion field in 3D). Langevin noise is added to the equations of motion to represent the thermal fluctuations. Accordingly, the model includes homogeneous and heterogeneous nucleation of growth centers [1, 2]. In addition to this, several mechanisms have been incorporated to form new grains at the perimeter of growing crystals, a process we term as “growth front nucleation” [3]. The equations of motion (three stochastic partial differential equations in 2D, and six in 3D) are solved numerically in a massively parallel environment. The model requires a detailed information on the system incorporating the free energy of the phases as a function of composition and temperature, the magnitude and anisotropy of the solid-liquid interface free energy and of the grain boundary energy, and the mobilities for the phase-, orientation and concentration fields, which are related to the translational, rotational and inter-diffusion coefficients. Advantages, problems and possible solutions for quantitative simulations will also be outlined. Numerous examples will be presented to demonstrate that the phase-field model supplied with orientation field(s) can successfully describe the formation of complex polycrystalline structures, such as impinging symmetric dendrites, disordered (“dizzy”) dendrites emerging as a result of dendrite-particle interaction, fractallike morphologies, and a broad variety of spherulitic patterns.
(ii) The phase-field crystal method is a recently developed atomistic approach that automatically includes competing crystal structures, defects, elasticity, and crystal anisotropies, and can be used to address the homogeneous and heterogeneous nucleation of competing crystalline phases, colloidal crystal aggregation, and solidification of alloys. After outlining the main features of the model, a few examples will be presented for its application such as amorphous precursor mediated crystal nucleation [4] and heterogeneous crystal nucleation [5].
[1] L. Gránásy, et al., Phys. Rev. Lett. 88, 206105 (2002)
[2] L. Gránásy, et al., Phys. Rev. Lett. 98, 035703 (2007)
[3] L. Gránásy, et al., Nature Mater. 3, 635 (2004)
[4] G.I. Tóth et al., Phys. Rev. Lett. 107, 175702 (2011).
[5] G.I. Tóth et al., Phys. Rev. Lett. 108, 025502 (2012).
Gábor Ribárik: Modeling of diffraction patterns based on microstructural properties
X-ray and neutron diffraction (XRD and ND) are powerful methods for investigating the microstructure of materials. The basic principles of the diffraction, the theory of size and strain broadening, the classical methods of the line profile analysis and the whole profile or pattern fitting methods: MWP and CMWP will be presented. The efficiency of these methods will be demonstrated by using real measurements. The latest 3D XRD method extended for line profile analysis will also be outlined.
Ádám Révész: Amorphous metallic alloys
There has been an increasing demand for high performance engineering components driving to the search for new advanced materials. Recently, a series of investigations on the formation and fundamental properties of bulk amorphous alloys were carried out. Amorphous materials lack any long term periodicity leading to different features compared to their crystalline counterparts. These amorphous structures exhibit supreme mechanical properties (high values of tensile strength, hardness, wear and corrosion resistance, fracture toughness, stored elastic energy and viscous flowability), exceptional magnetic and chemical properties (good soft magnetism, high frequency permeability and magnetostriction and high hydrogen storage).
In addition, the course will shed light on the microstructural characteristics and thermodynamics of this intensively investigated system.
12th July
Péter Nemes-Incze: Graphene: A two-dimensional carbon crystal
The talk aims to give an introduction to the properties of graphene, mainly from an experimental point of view. Building on our current knowledge and landmark papers in the field, I will review the charge transport, optical, mechanical, etc. properties of graphene and graphene nanostructures, such as nanoribbons. Emphasis will be put on current challenges and future avenues of research.
Ferenc Simon: Physics of single-wall carbon nanotubes: from introduction until the Tomonaga-Luttinger liquid state
Single-wall carbon nanotubes (SWCNTs) represent the one-dimensional form of carbon and their research remains a hot topic even after two decades since their original discovery. I shall give an introduction into the physics of SWCNTs including their discovery, geometry, electronic and vibrational structure. The SWCNT applications, synthesis methods, and modifications are also to be discussed. Finally, I will discuss the so-called Tomonaga-Luttinger liquid (TLL) behavior in SWCNTs from the point of view of the experiments. The TLL is an exotic correlated ground state of one-dimensional metals with a number of compelling properties.
Katalin Kamaras: Optical and Raman spectroscopy of carbon nanotubes
Optical properties of carbon nanotubes are of utmost importance both in basic
studies and with regard to applications. The optical spectrum directly
mirrors the electronic structure, both energy bands and excitons, on the
microscopic scale [1]. In macroscopic samples, the knowledge of the
transmission, refractive index etc. is essential when materials
properties have to be optimized.
There were many claims for applications of carbon nanotubes from electronic
circuits to elevators, but one clear success story is that of
transparent conductors manufactured from these systems [2]. Transparent
conducting layers are essential in many audiovisual applications today.
Inorganic oxides used for this purpose, as ITO (indium tin oxide) are
becoming rare and are toxic. Carbon nanotubes can act as natural
substituents to be used not only in optoelectronics but also for
biological applications where biocompatibility is crucial. With the
continous development of nanotube fabrication and separation methods,
samples enriched in metallic or semiconducting nanotubes can be
prepared. Electric conductivity, however, can also be improved by doping
with free carriers, e.g. hole doping by treatment with strong acids.
Depending on the wavelength range to be used, both methods can have
advantages and disadvantages, as high transmission and high conductivity
have to be balanced in one single film.
Raman spectroscopy is the method of choice when vibrational properties of
carbon nanotubes are to be studied. The unique radial breathing mode is
characteristic of the type of nanotube studied, thus even in macroscopic
samples the composition can be determined by this method. However, as
resonance effects complicate the picture because of the rich spectrum of
electronic excitations, special care has to be taken when determining
diameter and chirality distribution from Raman spectra.
In my presentation, I will introduce the basics of optical, infrared and
Raman spectroscopy of carbon nanotubes, and present the possibilities in
their study. I will concentrate on single-walled nanotubes since these
are the easiest to understand and interpret, but will show examples of
tubes filled with various molecules as well.
[1] Á. Pekker, K. Kamarás: Phys. Rev. B 84, 075475-1-8 (2011)
[2] Z.C. Wu, Z.H. Chen, X. Du, J.M. Logan, J. Sippel, M. Nikolou, K.
Kamarás, J.R. Reynolds, D.B. Tanner, A.F. Hebard, A.G. Rinzler: Science 305, 1273-1276 (2004)
Gábor Széchenyi: Zitterbewegung
The Zitterbewegung, which is a trembling motion of the center of the wave packet for relativistic free electron, was theoretically devised by Schrödinger in 1930. In 2005 Schliemann predicted that the Zitterbewegung is not only a relativistic effect, but can observable, in principal, for solid state physics, like graphene, semi conductors, 2D electron gases, spintronic systems.
We apply the general theory of Zitterbewegung to study the time evolution of the wave packets. At the end of the lecture we derive a relation between Zitterbewegung amplitudes and the frequency dependent optical conductivity.
14th July
Endre Tóvári: Introduction to electronic transport in nanostructures
Integrated circuits have undergone a tremendous miniaturization. At these extremely small sizes, already quantum mechanical effects must be taken into account, and the interference of electrons and interaction effects cause completely new effects, not seen in the macroworld.
In this lecture first I will give an introduction to the characteristic length scales, and discuss how the electronic transport changes in the different regimes. After that I will describe conductance quantization in the framework of Landauer formalism. At the end I will address some interference effects typical in nanostructures. All these topics will be illustrated with experimental examples.
Péter Makk: Introduction to molecular electronics
The idea that a single atom or molecule can function as the active part of an electrical unit is more than 35 years old, however, experiments have only turned this vision into a promising alternative during the last decade. Several interesting results, such as the conductance switching of molecular junctions by light irradiation or in-situ chemical reactions have been reported and even single molecule transistors, where large currents can be switched by putting a single electron charge on a molecule have already
been realized.
In this lecture I will give an introduction to molecular electronics. First an introduction to the experimental methods used to create molecular junctions will be given. I will review some of the basic methods which can be used to characterize these contacts (conductance histograms, vibrational spectroscopy, conductance fluctuations). Finally I will show some measurements on molecules acting as Single Electron Transistors.
References:
[1] T. Ihn.Semiconductor Nanostructures Quantum States and Electronic Transport. Oxford University Press (2010).
[2] J. C. Cuevas and E. Scheer. Molecular Electronics An introduction to Theory and Experiment. World Scientific (2010).
[3] Y. M. B. Yuli V. Nazarov. Quantum Transport Introduction to Nanoscience. Cambridge University Press (2009).
Dávid Szaller: Multiferroics: materials with unconventional properties
Materials exhibiting a simultaneous ferroic order of different degrees of freedom are called multiferroics. Among them, the most studied ones have both electrically and magnetically ordered ground states, called magnetoelectric multiferroics. In these compounds strong coupling between electric and magnetic degrees of freedom allows the electric control of the magnetization and the magnetic control of the electric polarization.
There is a broad range of applications for these materials including magnetic memories with low energy consumption. While the magnetic state can be used to store the information, in contrast to the conventional magnetic memories which can be written by applying a magnetic field, the information content of multiferroic memories also could be changed by external electric fields [1]. This process can be realised without dissipative currents.
The coupling between the electric and magnetic degrees of freedom is also manifested in the low-energy excitations. The collective modes of spins (spin-waves or magnons) in conventional magnetic crystals can only be excited by the magnetic component of the electromagnetic radiation, while in multiferroics they can be coupled both to the electric and magnetic component of light and are called electromagnons [2].
In materials simultaneously breaking time-reversal and spatial inversion symmetries the strength of absorption for two counter-propagating light beams can be different irrespective of the polarization state of light [3]. This effect is termed as non-reciprocal directional dichroism and until recent experiments on multiferroics [4] it was generally found to be weak. Our experiments showed a directional dichroism close to 100 % in the electromagnon excitation spectrum of the multiferroic materials Ba2CoGe2O7 and Ca2CoSi2O7 [5].
[1] T. Kimura et al., Nature (London) 426, 55 (2003)
[2] A. Pimenov et al., Nature Phys. 2, 97 (2006)
[3] W.F. Brown et al., J. Appl. Phys. 34, 1233 (1963)
[4] M. Saito et al., Phys. Rev. Lett. 101, 117402 (2008)
[5] S. Bordacs et al., accepted to Nature Phys.
János Asboth: Topological insulators: Insulators with a twist
One of the big successes of 20th century physics was the understanding
of how some materials conduct electricity, while others are electrical insulators. In a crystalline solid, if there is an energy gap separating the highest energy occupied state from the lowest energy unoccupied state, the solid is a (band) insulator. For a semiconductor in a strong magnetic field (the so-called Quantum Hall setup), however, this simple band theory of conduction breaks down. Although there is an energy gap in the spectrum, the samples conduct electricity at their edges, via so-called edge states. The conductivity of these samples is quantized, to within one part in a billion: this phenomenal precision is a subtle hint that there is some topological reason for the conductance.
Due to the periodic potential supplied by the atoms, the momentum of
an electron in a d-dimensional solid, instead of taking on any value in R^d, is confined to a d-dimensional torus. The texture of the electron states (spins and orbital pseudospins) on this torus can contain topological defects. Each topological defect in the torus describing the bulk gives rise to an edge state on the boundary of a sample.
Insulators with topological invariants associated to their electronic
bands, and associated edge states have been dubbed “Topological insulators”. During the last decade, intense research has shown that these materials not only have a number of fascinating properties, but, when combined with superconductivity, can also be useful to encode quantum information in a way that is protected from environmental noise. The first successful experiments in spring 2012 have already come in, showing that the basic building blocks (Majorana fermions) can be produced in the lab.
It might be that we are not very far away from constructing a complete “topological quantum computer”.
Lajos Diósi: Quantum and Gravity Together: Cosmic, and Nano?
According to standard views, these two dynamical concepts should interfere at very high energies and high mass densities occurring in relativistic cosmic phenomena only. Some, however, speculate that quantum and gravity meet in a new way already at nanoscales. These speculations emerged from the issue of wave function collapse in quantum mechanics, and has started to fuel a growing number of nano-experiments to test the quantum mechanical motion of objects which are far more massive than any objects tested ever before.
The lecture gives an elementary account of the above topics.
15th July
Dezső Beke: Nanobiengineering (definition, examples, biomimics in nanotechnology)
The nanobioengineering is a newly and fast developing research area. In the lecture first the definition of the Bioengineering will be given and the relation between bioengineering and other disciplines (physics, chemistry, informatics, biology, medical sciences etc.) will be treated. Then the special features of the nanobionegineering will be presented. In the second, part, based on our experimnetal investigations, examples of problems of nanoscale metal-ceramic bonding in dental materials will illustrated.
Róbert Horváth: Label-free optical biosensors for proteins and cells
Dezső Beke: Metal-ceramic bonding in dentistry
Ágnes Orbán: High-sensitivity diagnosis of malaria via magnetically induced linear dichroism
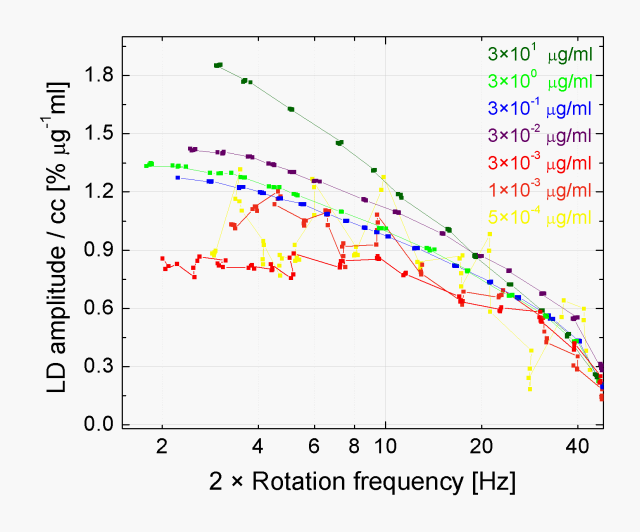
Although malaria infection is a global health issue, a cost-effective, yet highly sensitive diagnostic method has not been developed. We aim to design a compact and inexpensive clinical diagnostic device that could be operated without any expertise in the field of medicine or engineering. The principle of the detection – first suggested by Newmann and coworkers [1] – is the measurement of magnetically induced linear dichroism exhibited by malaria pigment (also known as hemozoin crystals), which is present in human blood only if infected by malaria parasites.These micrometer-size crystals are an appropriate target of diagnosis owing to their unique properties. As a consequence of their low-symmetry crystal structure and elongated shape, they exhibit large linear dichroism and magnetic anisotropy [2]. When suspended in blood, the magnetic anisotropy enables the single crystals to be orientated along their easy axis by an external magnetic field. This co-aligned ensemble of the dichroic crystals shows macroscopic linear dichroism for polarization along and perpendicular to the direction of the magnetic field. We studied this effect over the near infrared- ultraviolet region using a polarization modulation technique. As a more suitable alternative for diagnostics, we replaced the polarization modulation with a rotating magnetic field that forces hemozoin crystals to act like spinning polarizers. This concept –realized by the application of a
cheap laser diode, a Hallbach array magnet, a Rochon prism and a balanced photodiode bridge – provides an unprecedented sensitivity in the detection of malaria pigment corresponding to the minimal concentration of 0.5 ng/ml in blood plasma.
[1] D.M. Newmann et al., Biophysical Journal 95, 994 (2008).
[2] A. Sienkiewicz et al., J. Am. Chem. Soc. 128, 4534 (2006).